BOOLE’S ALGEBRA

Boolean algebra is an abstract algebra that operates with only the values ​​0 and 1 associated with the truth values ​​False and True (Boolean Logic). Algebra was developed in 1854 at University College Cork by Boole to write the logic of propositions in algebraic form. Today it forms the basis of the digital world. You study Boolean algebra or Boolean algebra because a digital circuit can be expressed through a boolean expression and vice versa (boolean logic). A Boolean function has one or more input variables and the output depends exclusively on the states assumed by the input, which we recall can only assume the values ​​zero and one. If we have n input variables as input, then all possible combinations are ²ⁿ and can be expressed by a table called truth table.

LOGIC CIRCUITS

Logic circuits are hardware components that manipulate binary information. The basic circuits are called LOGICAL GATE (logical gate). In order to describe the behavior of digital circuits, an algebra (mathematical notation) can be used which specifies the operation of each gate and allows the circuit to be analyzed and synthesized (drawn). Were identified and built electronic circuits that perform the elementary operations, these are called LOGIC GATES Logic gates are circuits that operate on multiple input signals and produce an output signal. They respond to two voltage range values ​​that we associate with the logical values ​​0 and 1. The logic gates representing AND OR and NOT operations are shown below. The variables are indicated with the letters A,B,C,X,Y,W,Z. The basic operations are AND ( • ), OR ( + ), NOT ( ¯ ).

Boolean functions are those functions of a Boolean variable that can only take on the values ​​true and false (1,0).

Example:

F=X+Y̅Z

We can represent the function using the truth table.

BOOLE’S ALGEBRA THEOREMS

DUAL

The principle of duality states that given one equality, another is obtained by replacing the AND operator with the OR operator, 1 with 0 and vice versa. Relations 1 and 2 are dual. De Morgan’s theorems are very important for obtaining the complement of an expression.

Proof of De Morgan’s theorem using a truth table.

The advantage of using Boolean algebra is that it allows simplification of digital circuits . Let’s see an example:

F=X̅YZ+X̅YZ̅ +XZ

F=X̅Y(Z+Z̅) + XZ By theorem 7) Z+Z̅ = 1

F= X̅Y+XZ

The two functions are equivalent, but the second function can be achieved with a simpler circuit.

DEFINITION OF COMBINATORY NETWORK

A combinatorial network is a logical network with n inputs and m outputs. The outputs are a function of the inputs, but not of the time: the inputs change and the outputs immediately change (obviously it is a model). In a logic circuit the logic gates are combined together forming a combinatorial circuit. Variables are combined using logical operations. We have seen that it is possible to express Boolean functions through its analytic expression or through the truth table. Boolean functions can be written in various ways but there are some expressions that are considered standard. To do this we define the minterms and maxterms.

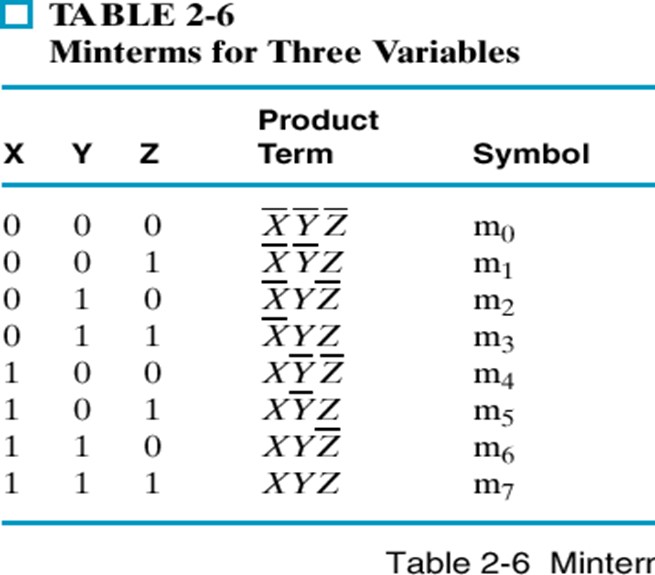
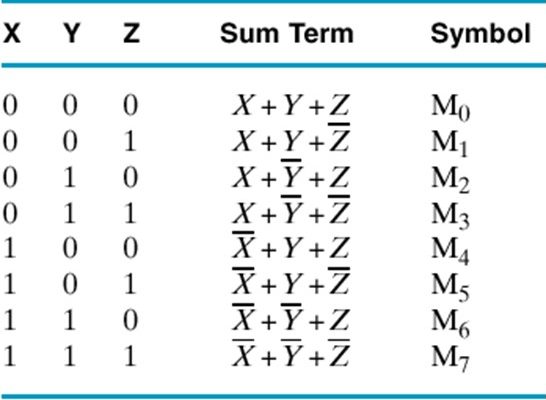
MINIMUM AND MAXIMUM TERMS

Considering a row of the truth table minterm is defined as the product of the Boolean variables relating to this row taken in direct or complemented form depending on whether they assume the value 1 or 0. Maxterm is defined as the sum of the Boolean variables taken in direct or negated form depending on whether they assume the value 0 or 1. With n variables we have ²ⁿ minterms and maxterms.

PRODUCT OF SUMS

We can obtain the analytic form of a function starting from the truth table as follows:

1. The rows for which F has the value 0 are identified;
2. As many sums are written as there are rows identified
3. Each sum is the max term related to the row
4. The product of the sums is done.

The advantage of the standard forms is that of allowing the realization of the functions with two-level circuits: AND-OR or OR-AND.

KARNAUGH MAPS

The Karnaugh map is an exact representation method of synthesizing one or more level combinatorial networks. Such a map constitutes a visual representation of a Boolean function capable of highlighting the pairs of min-terms or max-terms with a unitary Hamming distance (that is, of terms that differ by a single binary (or Boolean) variable). Since they derive from a less intuitive vision of Boolean functions in spaces {0,1} ⁿ with n number of variables of the function, Karnaugh maps are effectively applicable only to functions with at most 5 – 6 variables. A Karnaugh map is a graphical method that aims to reduce the complexity of Boolean functions expressed in canonical forms. It is built starting from the truth table of a Boolean function, in the process of synthesis of a combinatorial network. Karnaugh maps simply allow the minimal form of a function to be constructed as a sum of logical products (disjunctive form) or as a product of logical sums (conjunctive form) and therefore simplifications of the Boolean function often more immediate than those obtainable with algebraic modifications.

SIMPLIFICATION OF A FUNCTION

Since there are 16 combinations of the 4 boolean variables, the Karnaugh map must also have 16 positions. The most convenient way to arrange them is in a 4×4 table. The binary numbers in the grid show the function’s output value for all possible input combinations. We will write 0 at the top left since f = 0 when A = 0, B = 0, C = 0, D = 0, i.e. f(0,0,0,0) = 0. Similarly we will write 1 in the lower right since A = 1, B = 0, C = 1, D = 0 return f = 1, i.e. f (1,0,1,0,) = 1.

METHOD

After constructing the Karnaugh map, the 1s are grouped into the largest possible rectangles, which however always have an area (in squares of the table) equal to a power of 2 (1, 2, 4, 8, 16, 32, … ). The optimal groupings, in this example, are those indicated on the map with the green, red and blue outline. For each grouping we find the variables that do not change their value. For the first grouping (the red one) we see that: Variable A maintains the same state (1) throughout the group, therefore it must be included in the resulting product. Variable B does not hold its value, going from 1 ( f(1, 1,0, 0) ) to 0 ( f(1, 0, 0, 0)), and therefore must be excluded. C doesn’t change, it keeps the same state (0), so it is included. D changes and is excluded. Thus the first product that will be part of the final Boolean expression is AC̅ (the direct variable is considered if, for the values ​​inside the rectangle, it assumes the value 1, and its negated if instead it assumes the value 0). For the green rectangle (formed by four 1s arranged vertically) we see that A, B maintain the same state, while C and D change. Since B equals 0, the variable must be negated before being included in the product. Thus we obtain AB̅. With the same procedure, BCD’ is found in the blue rectangle: the only variable that should not be included in the product is A as it changes value within the rectangle. The final expression of the function f is obtained by adding the products previously found: AC̅ + AB̅ + BCD̅. If one wants to find the dual function, i.e. the function that makes use of the maxterms, it is enough simply to group the values ​​0 instead of 1: this corresponds to choosing in the truth table the rows for which the output function is 0 instead of 1. In this case, the variables that remain constant in the grouping and that have a value of 1 must be complemented (i.e. negated). In the example shown the dual function is given by (A+C) (A+B) (B̅+C̅+D̅). In a Karnaugh map with n variables, a Boolean product of k variables corresponds to a rectangle formed by ^2n-k boxes. Karnaugh maps are also suitable for simplifying functions that contain conditions of indifference (don’t care, i.e. input values ​​for which it is irrelevant what the output is): these are usually represented in the grid with the symbols *, – or with the Greek letter (delta), and can be considered both as 1 and as 0, so as to form larger groupings. However, groupings of just don’t care are not allowed.

Note: The grid is to be considered, not as a plane, but as a torus, therefore the rectangles can cross the edges, both vertically and horizontally, passing from one side to the opposite one. For example, ABD̅ could also be a valid product.

FURTHER INFORMATION

BOOLE’S ALGEBRA